Harry Potter vertrekt met de trein vanaf platform 9 ¾ en dat is om meer dan één reden een heel goede illustratie van wat een fractal is. Een fractal is een meetkundige figuur die opgebouwd is uit delen die min of meer gelijkvormig zijn met de figuur zelf. Fractals hebben een oneindige hoeveelheid details, en bij sommige fractals komen motieven voor die zich op steeds kleinere schaal herhalen. Doorgaans kunnen fractals gegenereerd worden door het herhaald toepassen van een bepaalde bewerking. De term fractal werd geïntroduceerd in 1975 door B. Mandelbrot en is afgeleid van het Latijnse fractus (gebroken). Wiskundige objecten met fractale eigenschappen werden eind 19e en begin 20e eeuw ontdekt. De bekendste fractals zijn de Mandelbrot-verzameling en de Juliaverzameling.

In de gewone meetkunde is een rechte lijn één-dimensionaal, een vlak twee-dimensionaal en een ruimtelijke vorm drie-dimensionaal. Voor fractals kan de dimensie niet zo eenvoudig aangegeven worden. Mandelbrot constateerde dat de meeste fractals een niet-geheeltallige dimensie hebben, die fractale dimensie wordt genoemd. De dimensionaliteit van sommige figuren is zo voor de hand liggend dat het niet nodig lijkt een methode bij de hand te hebben om de dimensie te bepalen. Zo is een rechte lijn ‘duidelijk’ een-dimensionaal en een plat vlak twee-dimensionaal. Hij ontwikkelde een formule om het aantal punten te berekenen om daaruit de dimensionaliteit vast te kunnen stellen, die ik hier buiten beschouwing laat. Voor lijnen en vlakken was dit simpel, maar niet voor de verzameling punten op bijvoorbeeld een wolk of een kustlijn. Deze blijken niet precies twee- of drie-dimensioneel te zijn, maar 2,3 of 1,2. Dit soort figuren waarvoor de dimensie niet een geheel getal is, heten fractals.

Op deze droge, en wiskundig zeer abstracte wijze, lijkt er niet zo veel aan de hand. Maar als Randall kan vaststellen dat er vele dimensies in ons universum naast elkaar bestaan. En dat er zelfs gebroken dimensies bestaan, die naadloos aan elkaar sluiten en zelfs in elkaar overgaan. Dan kun je beginnen voor te stellen dat de gladde mooie dimensie waar wij ogenschijnlijk in leven helemaal niet bestaat. De 3D werkelijkheid is maar een eenvoudige theoretische weergave. In de werkelijkheid bestaat er een oneindig continuüm van dimensies waar wij in leven. Niet alleen als fysiek drie-dimensioneel lichaam, maar als multi-dimesioneel wezen. Dat we daar zijn is niet voorbehouden aan sjamanen, wonderdoeners en heiligen. Een heel groot stuk van onszelf leeft tegelijkertijd in al die dimensies. Daar zit onze blauwdruk, daar zitten de codes van ons herstel. Daarvandaan doen we aan onszelf wonderen verrichten. En daardoorheen vertrok Harry Potter met de trein.

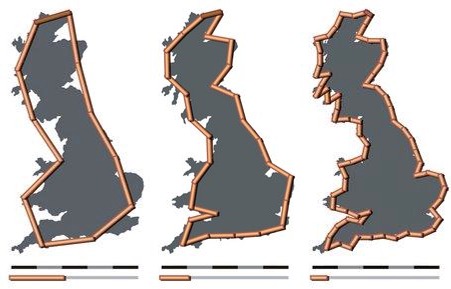
De uitleg van het gebroken zijn van een dimensie wordt prachtig geïllustreerd met de opdracht aan studenten cartografie. Het opmeten van de lengte van een kustlijn. De lengte blijkt afhankelijk van de lengte van je liniaal, om het maar zo uit te drukken. Een steeds kleinere liniaal levert een steeds langer gemeten kustlijn. De kustlijn heeft dus geen definitieve lengte en is daarmee geen glad afgebakende hele dimensie.